Maybe you are more at home in programming languages like C#, Java or Visual Basic. If this is the case, you are probably familiar with the programming structure of loops. This concept may even have become flesh and blood so much that you often use it "automatically" to solve your problems. It could even be that you are working intensively with the M-Language for the first time and are now also trying to reach your goal with this approach in Power Query or Power BI?
In M, however, you will encounter a completely different programming paradigm. The M-Language is a functional language for which the classical loop constructions of other languages are foreign. As a basic element for repetition of expressions, functional programming languages use recursion instead, and the M-Language also offers this feature. In addition, M has other functions with which you can simulate loop-like behavior.
Even if such constructions in functional languages should not be the first, but rather one of the last means of choice, it is good to know that they are also available to you in M in case you need them. In this series of articles, we will take a look on how this works.
In the first part of the series I will show you how to create recursive functions in M. In the second part we will take this concept to the next level and take a look at the function List.Generate(). The third and last part will discuss some use cases of the function List.Accumulate().
How do recursive functions work in M-language?
Recursive functions are functions that repeatedly call themselves within their own function definition. The best way to illustrate this is to take a look at the following example:

The function "fnXmultiplizieren" ("fnXmultiply")
expects the value x as number (green part) as single parameter. In our example we simply assume that the value 4 is passed to the function.
The function checks this value for the fulfillment of a specific criterion, in this case whether x is greater than 150 (yellow part). If this criterion is fulfilled, the current value of x is set
to be the output of the function.
If the criterion is not fulfilled, the red part of the function kicks in. In that part, the function "fnXmultiplizieren" is called again. This happens because the function name is preceded by the so-called Scoping-Operator @. Since the function expects us to a parameter to the function, the value x multiplied by 3 is injected again. This process is repeated until the criterion in the yellow part is fulfilled, i.e. the value passed on the repeated call is greater than 150. In that case the red part of the function no longer will be executed and the current value of x is set to be the output. In the picture above you can see that this happens after four loops when the value of 324 is reached.
In order to generate a recursive function in M, you need three essential components:
- A user-defined M function in which the recursion is to be performed.
- An abort criterion, often generated by an "if then else" expression, which aborts the recursion as soon as the desired condition is met. This prevents infinite loops.
- The Scoping operator @, which tells the function to call itself as long as the abort criterion is not met.
In this way, you can create programming structures in M that work according to the principle of "Do-Loop" or "While-Wend" loops known from other languages.
What else can recursive functions do for you? Of course it is not just about counting up numbers with recursive functions. Finally, you can use all standard functions that M offers in your recursion. Accordingly, in recursive functions you have the possibility to edit or handle all kinds of values, may it be tables, lists or records.
On the web you will find a number of inspirations for the use of recursive functions. Ivan Bondarenko shows an example for the processing of Parent-Child hierarchies with the help of recursive functions on his blog. Another example is this forum post on "Stack Overflow", in which a table is automatically extended by various index columns.
So there are hardly any limits to your imagination.
Why do recursions work in M at all?
If you are a little familiar with the environment concept of M, you might wonder why recursive calls within functions work at all? The environment concept of M makes statements about the scope of values or named values, called variables, within your M code. Basically it specifies under which circumstances variables in M can access each other. Strongly simplified, it says that variables can only access variables that are in their environment or in the environment of their superordinate expression. The variable itself is not contained in its own environment, so it cannot access itself! If this statement is true, how can recursive functions do just that?
If you want to learn more about the basic principles of the environment concept in M, I recommend a series of articles by Lars Schreiber and Imke Feldmann. Their series on this topic is by far the best summary for this important subject that I have ever read: The Environment concept in M for Power Query and Power BI

In principle, of course, the previous statement remains valid. We just have to add another special case. In addition to the environment of a variable very briefly described above, "Let" expressions and record initializations create a second environment, namely one in which the initialized variable itself is contained. This also happens when we call the function in our example, as shown in the picture on the left. For the variable "Quelle" ("Source") or the function "fnXmultiplizieren" assigned to it, an additional environment is created in which the variable itself is present.
Variables, tables, queries, functions and other values in M are referenced by their name, their "identifier". In the case of our sample function, this is via the identifier "fnXmultiplizieren". For an identifier reference, however, a distinction can be made between two types:
The name "fnXmultiplizieren" is a so-called "Exclusive-Identifier-Reference", i.e. one from which the function itself is excluded. However, there are also
"Inclusive-Identifier-References". These allow access to the version of the environment that contains the initialized variable itself.
How can you now convert "Exclusive-Identifier-References" into "Inclusive-Identifier-References"? Quite simply, this is done by prefixing the identifier using the Scoping operator
@, i.e. by writing "@fnXmultiplizieren".
What are the drawbacks of recursive functions ?
As already mentioned at the beginning, I recommend to use recursions in M only as a last solution for a problem, if there is no standard function available to get the job done. The performance of your code suffers enormously if, for example, you iterate over all lines of a table to identify the lines for further processing based on a certain criterion. The standard function Table.SelectRows() would be the better choice. This is just one of many conceivable examples and it is only intended to illustrate that the processing of entire sets of data using standard functions should be preferred to the individual handling of rows using recursion.
But if recursive functions are still the means of choice, you should consider the following limitation:
Recursive functions in M do not support "tail call elimination". What does that mean? At least that's what I asked myself the first time I heard about it:
This topic always is relevant when the last instruction of a function is a call of a function again, as it is the case in our examples. Put simply, for functional languages, a function is evaluated by lining up the function call on your computer in a kind of queue. This queue is called the "Call Stack" and processes the individual function calls before it is emptied again at the end. However, the "Call Stack" cannot queue an unlimited number of function calls. At some point its capacity is exhausted.
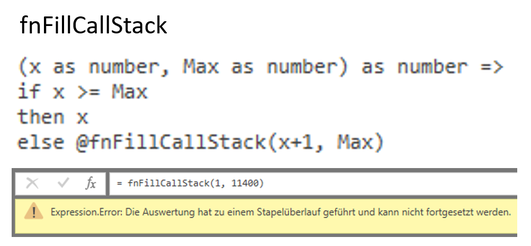
The picture above shows the function
"fnFillCallStack" that was executed as an example. The function expects two parameters. The number x, which is the start value, and the value "Max", which contains the maximum number
of recursions the function should execute. In each loop, the value x simply is increased by 1. If we set x=1 and Max=1000, x is increased by 1 until 1000 is reached.
In my case I could observe that the function was terminated with the error shown above starting from approx. 11,400 recursions, due to hitting the limit of the
"Call Stack".
Programming languages that support "tail call elimination" do not occupy a place in the "Call Stack" for every function call. Rather, when the function is called again, the space of the previous call is released and only the current call is kept in the queue. In this way, a function can have a greater recursion depth and always occupies only one constant place in the "Call Stack".
In summary, you should keep in mind that in addition to comparatively poor performance, the use of recursive functions in M can even lead to the failure of your entire data transformation process when you hit the limit of your call stack.
What we have learned and how we will proceed?
The generation of loops in M can be achieved relatively easy with the help of recursive functions. All you need is a
custom function, an abort criterion for the function and the scoping operator @.
You should be careful not to use recursion in M lightly, because the use can have negative impact on the performance and even lead to the complete failure of your data
transformation process due to overflow of call stack.
You can overcome this drawbacks using some standard functions like List.Generate() or List.Accumulate() instead and should
therefore use them preferably. How this works I will show you in the following parts of this series.
There is more to come! Take a look at the other parts of the series:
I hope you liked the article and will also read the other parts of the series. If that's the case, please also don't forget to share this article with other people!
See you next time!
Many greetings from Hamburg
Uwe




Kommentar schreiben
Alejandro Bedoya (Sonntag, 13 September 2020)
Mil gracias por la información es muy practica para lo que quiero realizar.
Dr. Ralf Röhrig (Freitag, 11 Dezember 2020 16:09)
Very usefull information, especialy for beginners in M, and very clear explanation.
Dino Antunes (Samstag, 03 Juli 2021 15:19)
Dear All
Very Very good, can you provide please pratical examples in excel to improve my skills.
Thanks in advance
Dino
Gustavo Moraes (Mittwoch, 22 März 2023 23:26)
Excellent series! Very well written text. Learned a lot from it.
Thank you very much!